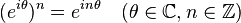ド・モアブルの公式

ド・モアブルの定理（ド・モアブルのていり。ド・モアブルの公式（ド・モアブルのこうしき）とも）とは、複素数（特に実数） θ および整数 $n$ に対して

(\cos \theta +i\sin \theta)^n=\cos n\theta +i\sin n\theta

が成り立つという、複素数と三角関数に関する定理である。定理の名称はアブラーム・ド・モアブル (Abraham de Moivre) に因むが、彼がこの定理について言及したわけではない^[1]。帰納法による証明では、三角関数の加法定理が利用される。

実数 θ と正の整数 $n$ に対してド・モアブルの定理を考えると、左辺を展開し右辺と実部・虚部を比較することにより、 $n$ 倍角の公式が導出される。すなわち、ド・モアブルの公式は三角関数の $n$ 倍角の公式を内在的に含んでいる。

オイラーの公式 : $(e^{i\theta})= \cos\theta+i\sin\theta$ によれば、この定理は複素変数の指数関数に関する指数法則（の一つ）

(e^{i\theta})^n=e^{in\theta}\quad(\theta \in \mathbb{C},n \in \mathbb{Z})

の成立を意味するものである。